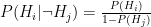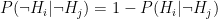In cryptographic attacks, we often rely on abstracted information sources which we call “oracles”. Classic examples include the RSA parity oracle attack, which depends on an oracle disclosing the least-significant bit of a ciphertext’s decryption; Bleichenbacher’s attack on PKCS#1v1.5 RSA padding, which depends on an oracle for whether a given ciphertext’s decryption is correctly padded; similarly, the famous padding oracle attack on CBC-mode encryption; or the commonly-seen MAC forgery attacks enabled by non-constant-time MAC validation.
In all of these cases, the attacker finds a way to compound small information leaks into a break of the system under attack. Crucially, in principle, the source of the leak doesn’t matter for the attack: the oracle could come from overly verbose error messages, from timing side channels, or from any other observed property of the system in question. In practice, however, not all oracles are created equal: an oracle that comes from error messages may well be perfectly reliable, whereas one which relies on (say) timing side channels may have to deal with a non-negligible amount of noise.
In this post, we’ll look at how to deal with noisy oracles, and how to mount attacks using them. The specific cases considered will be MAC validation and PKCS7 padding validation, two common cases where non-constant-time code can lead to dramatic attacks. However, the techniques discussed can be adapted to other contexts as well.
Preliminaries
Our primary tool will be Bayesian inference. In Bayesian inference, we start with a prior probability distribution for the value of some unknown quantity, and we use Bayes’ theorem to update this distribution based on experimental observations.
In our case, the unknown quantity will be a single byte, and the observed data will be the outputs of the noisy oracle. We’ll start with a uniform prior over all 256 possible values, which we will update as we make queries. We will look at a few strategies for making queries, see how they affect the resulting posterior distribution, and compare their performance.
This post is not intended as a math tutorial; readers unfamiliar with the terms used above are gently suggested to review the relevant Wikipedia articles: Bayesian inference and Bayes’ theorem. There is also a very nice video on Bayes’ theorem from 3Blue1Brown, which may be more accessible.
If you’re looking for a primer on the padding oracle attack, I also have a blog post on that topic.
Regarding the noisy oracle itself, we will assume that its noisiness is constant, and that we can measure it. These assumptions both could, in principle, be relaxed somewhat, but they simplify the presentation, and hopefully the reader who wants to generalize the given technique to the more general case will be able to see how to do so.
Let’s be more precise with what we mean by “noisy”: a noisy oracle is one that gives us a correct answer some of the time, but not all the time. Let’s call the false positive probability 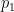 and the false negative probability
and the false negative probability 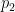 . To be clear, these are conditional probabilities: the probability that a positive result is a false positive, and that a negative result is a false negative, respectively. In some cases we may have
. To be clear, these are conditional probabilities: the probability that a positive result is a false positive, and that a negative result is a false negative, respectively. In some cases we may have 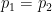 , but in general there is no need to assume this.
, but in general there is no need to assume this.
Math
First, let’s recall Bayes’ theorem, which we will use to update our prior distribution. Let 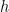 be a hypothesis, and
be a hypothesis, and  be some evidence on that hypothesis. Then Bayes’ theorem says that
be some evidence on that hypothesis. Then Bayes’ theorem says that
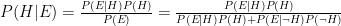
Both of the attacks mentioned above (padding validation and MAC validation) apply the oracle to a byte search. We scan through 256 candidate bytes, one of which has a property that the rest of the bytes do not have, which our oracle is (at least sometimes) able to detect. In both cases, we start from the assumption that each byte is equally likely to satisfy our test.
To put this into notation, we have 256 hypotheses, 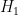 through
through 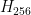 . Initially, we start with a uniform distribution:
. Initially, we start with a uniform distribution: 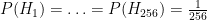 .
.
We’ll use 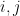 for list indices. We have
for list indices. We have 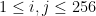 and
and 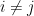 .
.
We can get two kinds of evidence: 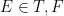 depending on whether the oracle gives us True or False on some query for some byte. We can subscript this by the index of the tested byte; in practice, this’ll just be
depending on whether the oracle gives us True or False on some query for some byte. We can subscript this by the index of the tested byte; in practice, this’ll just be 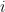 or
or 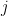 depending on whether the byte we’re testing corresponds to the hypothesis we’re considering. So we need to be able to evaluate probabilities for
depending on whether the byte we’re testing corresponds to the hypothesis we’re considering. So we need to be able to evaluate probabilities for 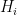 together with
together with 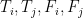 .
.
Now, let’s do some case work as we expand each of the terms in Bayes’ theorem:
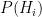 starts at
starts at 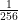 and gets updated on each oracle query.
and gets updated on each oracle query.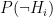 =
= 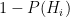 .
.
- Cases where subscripts match:
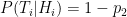 (true positive)
(true positive)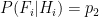 (false negative)
(false negative)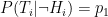 (false positive)
(false positive)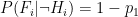 (true negative)
(true negative)
- Cases where subscripts differ:
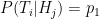 (false positive)
(false positive)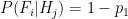 (true negative)
(true negative)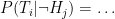 (could be true or false positive)
(could be true or false positive)
- Probability of true positive:
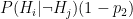
- Probability of false positive:
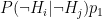
- Probability of true positive:
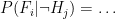 (could be true or false negative)
(could be true or false negative)
- Probability of true negative:
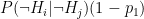
- Probability of false negative:
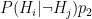
- Probability of true negative:
Clear? Good. Let’s move on.
Strategy
We’ll consider three different strategies for making queries:
- Exhaustive: We will make a large number of queries for each byte. We will simply loop through all 256 bytes, querying each one, until one of them reaches the target confidence threshold. This is the simplest and most commonly recommended strategy; it is also by far the least efficient. It does not adapt to the results of previous queries, and it requires a very large number of oracle queries.
- Information-guided: We will estimate the expected information gain from each possible oracle query, then choose the query with the greatest expected information gain. This requires us to compute 512 posterior distributions per step and measure each distribution’s entropy; this does require significantly more local computation. However, this scheme is still a big improvement over the previous one.
- Probability-guided: We will always query for the byte whose hypothesis has the highest estimated probability. This has much lower compute overhead than the information-guided strategy; in terms of performance, the comparison is very interesting and we will discuss it in detail below.
Implementation
Let’s codify all of the above into a Python class, ByteSearch. We’ll implement the math, but we won’t start there; first, let’s just encapsulate that complexity within a self.get_updated_confidences method which updates our priors based on the results of a single oracle query. Then we can define the following scaffolding:
The idea is that calling code would invoke search() on an instance of this class, passing in something like the instance’s pick_by_confidence or pick_by_entropy bound method as an argument. The above code depends on a few static methods which encapsulate the mathematical machinery:
The bayes method implements Bayes’ theorem. The get_updated_confidences method implements the math we discussed above. The get_entropy method computes the entropy of a distribution. These static methods, together with the previous snippet, provide a full implementation for ByteSearch. You can find a test script which defines this class and uses it to run a padding oracle attack here.
Performance
In order to carry out a full attack, which requires recovering 16 bytes in a row without any errors, we need each individual byte search to return an accurate result with high probability. If our confidence in a single search’s correctness is  , then our confidence in the success of the overall attack is
, then our confidence in the success of the overall attack is 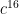 . Even if
. Even if  is large,
is large, 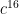 may not be: e.g.
may not be: e.g. 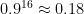 ,
, 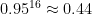 , and
, and 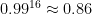 . Even
. Even 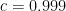 gives an overall failure rate of roughly 1.5%.
gives an overall failure rate of roughly 1.5%.
In the following measurements, I used 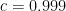 . I set the false-positive and false-negative rates to 0.4; in other words, the oracle gives the correct answer only 60% of the time. There is nothing special about this value, and it could be lower – I’ve successfully tested the code with accuracy rates as low as 50.1% – but I thought 60% is both low enough to be interesting and high enough to be practical.
. I set the false-positive and false-negative rates to 0.4; in other words, the oracle gives the correct answer only 60% of the time. There is nothing special about this value, and it could be lower – I’ve successfully tested the code with accuracy rates as low as 50.1% – but I thought 60% is both low enough to be interesting and high enough to be practical.
For a baseline reference, with a perfect oracle, a padding oracle attack on a 16-byte block of ciphertext is expected to require an average of 128 queries per byte, giving a total of 2048 oracle queries to complete the attack in the average case, and 4096 queries in the worst case.
In comparison to these roughly two thousand queries, the exhaustive strategy described above is able to complete the attack, with per-byte confidences of 0.999, in an average of about half a million unreliable oracle queries. This is quite a bit more overhead: our number of oracle queries has increased by a factor of roughly 250. To be fair, we’ve gone from a perfect oracle to a very unreliable one, so perhaps some credit is due for the fact that we can complete the attack at all. But even so, this is a lot of overhead – and it turns out we can do much better.
The entropy-guided strategy performs better in terms of oracle queries; however, while it uses fewer queries, it comes at the cost of much higher CPU overhead. This workload parallelizes trivially, but a naive implementation like the one given above is very slow and is not recommended in practice.
Perhaps surprisingly, the probability-guided strategy performs best of all, completing in an average of just over fifty thousand queries. This is roughly a tenfold improvement over the exhaustive strategy, and is several times better than the entropy-guided strategy, despite following a simpler and more naive heuristic. This strategy is recommended in practice. But why does it work so much better?
Analysis
In this section I’d like to share some illustrations of each strategy in action. These take place in a simplified setting: we have a search space of size 16 (and if this
reduction bothers you, try thinking of it as a hex digit being checked by a non-constant-time string comparison), and our false-positive and false-negative rates are both fixed at 0.25, giving a 75% accurate oracle. These changes make the search terminate faster and help it fit better on screen. In each search, the target digit is 0x8 (so, the 9th column).
On the left, I’ve included two charts: the first one indicates the Bayesian confidence levels for each digit, and the second one indicates (on a log scale) the expected information gained by querying for that digit. Stated differently, this chart shows the expected reduction in entropy in the confidence distribution after the given query.
Let’s start with a look at exhaustive search. Whenever someone tells you “just make more oracle queries”, this (or – even worse – its depth-first analogue) is usually what they’re recommending. The inefficiency should be obvious.
Note how many oracle queries get wasted on confirming things that we basically already know, e.g. ruling out digits that already have very low confidence.
Now that we’ve seen the worst strategy, let’s see the best one:
This video includes a few runs of the search with different RNG seeds. Note how this strategy essentially dives in as soon as it finds a promising option, taking a very “depth-first” approach to exploring the search space. Intuitively this seems well-matched to the problem at hand.
Finally, we’ll look at the middle option, which happens to exhibit some different behavior from the others. In this one, rather than being guided by confidences, we are guided by expected information gained, which is simply computed by computing the Bayesian adjustments that would occur if an oracle query for a given digit returned true or false, taking an average of the entropies of those distributions weighted by their estimated probabilities (using our current confidence levels), and taking the difference between this and our current entropy; in effect, this chooses the query which is expected to minimize post-query entropy in the confidence distribution.
This exhibits some interesting behavior that we don’t see in the other strategies: it is capable of rapidly honing in on promising options, much like the confidence-guided strategy, but it does not do so immediately, even if it gets an initial positive result from the oracle. Instead, it prefers a more thorough, somewhat breadth-first approach which stands in heavy contrast to the confidence-guided strategy (which may not even end up querying for every digit, if it finds a promising one early enough).
The reason for this difference may not be immediately obvious, but it turns out to be simple: while initial positive results are promising, they also carry a degree of risk, because they can be undone: a subsequent negative response from the oracle for the same digit (which is still considered much more likely than not) would reset the digit’s confidence level close to baseline, actually increasing the distribution’s entropy. In contrast, querying other digits about which less is known carries a similar level of upside but much less downside, so these options end up being favored, at least until we’re able to rule them out as frontrunners.
As I said above, this is just a starting point, and there are other metrics that could be used here (e.g. it might be interesting to try using Kullback-Leibler divergence rather than simple arithmetic difference between confidence distributions). But among these options, the confidence-guided strategy stands out as a clear frontrunner, and performs much better than the other strategies, especially as the error rate gets close to 50%. If it finds a promising digit early on, it hones in on it, and it is willing to accept small incremental progress in order to refine its estimate about the frontrunner, which ultimately is what is necessary to cross the confidence threshold quickly; however, in spite of this focus on speed, it remains very reliable and can refine its results to arbitrary levels of confidence.
Conclusions
Presentations of oracle-based attacks typically assume a perfect oracle; if the noisy-oracle case is treated at all, usually it is assumed that a perfect oracle will be simulated by increasing the noisy oracle’s sample size to the point where its error rate is negligible in practice. This strategy, while simple, is wildly inefficient. In this post, I have shared some strategies for reducing the number of oracle queries required to complete some common attacks. These strategies do not seem to be too widely known; I have not seen them discussed, and all of the above work was derived independently. I hope that this post will help to popularize these strategies.
In closing, I would note that there are opportunities for follow-up work applying these methods to other common oracle-based attacks, as well as relaxing some of the simplifying assumptions outlined above.
I’d like to thank Giacomo Pope, Kevin Henry, and Gerald Doussot for their feedback on this post and for their careful review. Any remaining errors are mine alone.